Contents
Introduction
Hypothesis Testing of Female Voting
Type 1 and Type 2 Errors
Hypothesis Testing of Voter Education
Key Questions For 2024
Concluding Remarks
Other News In Geopolitics This Week
Bitesize Edition
Last week, I provided a large amount of data on the 2016 and 2020 elections. Under this data, there are many trends in voting behaviour that we can explore. I’m going to do that today through a process called hypothesis testing.
I’ll explore the behaviour of female voters in 2016 and 2020. Donald Trump has a history of misogyny, and so do female voters who prefer to vote for any other candidate but him. Also, did Clinton or Biden gain a significant amount of support from female voters?
In a topic with more data availability, how does education level align with voting patterns? My hypothesis is that a higher education of a voter implies this voter has a higher likelihood of voting Democrat. Does the data support this?
Introduction
It’s clear from many subsets of the data that we explored last week, that there exists some evidence for trends underlying the data. This week, I’m going to explore two of those trends via a process called hypothesis testing. I’ll explore whether women are more likely to vote Democrat rather than Republican, and if higher-education voters show greater support for Democratic candidates versus Republican candidates.
Hypothesis Testing of Female Voting
A hypothesis is a predicted answer to a research question based on existing knowledge. Importantly, this hypothesis can be tested based on sample data, which I will do today based on the data from last week’s Geopolitics Review.
The process is as follows:
Define the hypothesis/prediction
State the error percentage under which we reject our prediction. This is known as the significance level.
Collect data.
Analyse the data via a suitable test. Today, I’ll be using the chi-squared test.
Calculate your degrees of freedom. I’ll explain how we do this below but it is based on the size of our dataset.
From this, we can calculate our p-values. We want a p-value lower than the significance level because this means there is evidence to support our prediction.
Interpret these results.
Let’s start with an example.
Hypothesis: Women are more likely to vote Democrat than Republican.
Null Hypothesis H(0) = Women voters show no preference towards Democrats over Republicans.
Alternate Hypothesis H(1) = Women are significantly more likely to vote Democrat than Republican.
The null hypothesis H(0) usually states a level of equality. In this case, that equality refers to no preference between female voters for Democrats and Republicans. The alternate hypothesis H(1) is the opposite of this, with women being more likely to vote Democrat than Republican. The hypotheses are opposites so only one hypothesis can be true at a time.
Significance Level = 5%. This is the probability that we make an error when failing to reject or rejecting the null hypothesis, H(0).
Note, that we don’t accept H(0), we fail to reject. This is because our hypothesis test doesn’t imply complete truth. It states that the data supports the prediction, hence we fail to reject it.
We will later use our significance level of 5% to reject or fail to reject our H_{0}.
Type 1 and Type 2 Errors
A Type 1 error occurs when we reject H(0) but the data supports the hypothesis. In this case, we would reject that women have no preference towards Democrats or Republicans, but the data would actually support that women show no preference towards Democrats or Republicans.
A Type 2 error occurs when we fail to reject H(0), but it’s a false prediction. In this case, we would fail to reject that women have no preference to vote Democrat than Republican, even though the data supports that women are significantly more likely to vote Democrat than Republican.
It’s important we’re aware of these errors so we stand a better chance of recognising them when they occur.
With these potential errors in mind, let’s continue with the process.
In our hypothesis test, we will be using the Chi-squared Test. The specific tests used are based on the nature of the data, the sample size, and the characteristics of the test being performed. Other tests include the student t-distribution or the z-test.
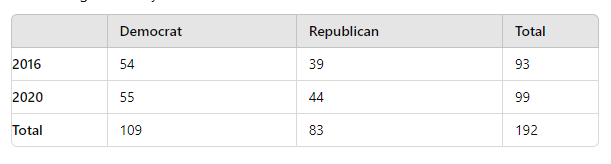
The Chi-squared test may only be carried out on actual numbers, and hence we will assume a sample of 100 voters and use the percentages in the datasets above to attribute to a number of voters for Democrats and Republicans.
The Chi-Squared Formula is as follows:
O = Observed Frequency (Our Dataset)
E = Expected Frequency (Calculated)
Woman Votes Democrat In 2016: (93*109)/192 = 52.80
Woman Votes Republican In 2016: (93*83)/192 = 40.20
Woman Votes Democrat In 2020: (99*109)/192 = 56.20
Woman Votes Republican In 2020: (99*83)/192 = 42.80
Using the formula above:
We then take the number of columns and rows of our table to calculate the degrees of freedom. We have two rows and two columns, and calculate degrees of freedom as such:
Where r is the number of rows and c is the number of columns. In this case, our degrees of freedom would be equal to 1.
Taking this and our test statistic of 0.12236, we achieve a p-value of 0.7265.
We hence failed to reject H(0) and so believe there is no preference of female voters to either Democrats or Republicans. We made these decisions using the significance level of 5% we chose earlier.
A P-value of less than the significance level of 5% would have shown there is sufficient evidence to reject our null hypothesis. It’s worth noting that if we have more data, we can have more confidence in our results. If we believe in our prediction, more data could also help to confirm our prediction. I’ll now explore a hypothesis involving voter tendencies based on their education. In this test, we have more data.
Hypothesis Testing of Voter Education
Hypothesis: More educated means more Democrat-aligned.
Keep reading with a 7-day free trial
Subscribe to Geopolitics Explained to keep reading this post and get 7 days of free access to the full post archives.